We move the blogs on this research front to our Group-Blog-Site at https://qdata.github.io/qdata-page/ since 2021.
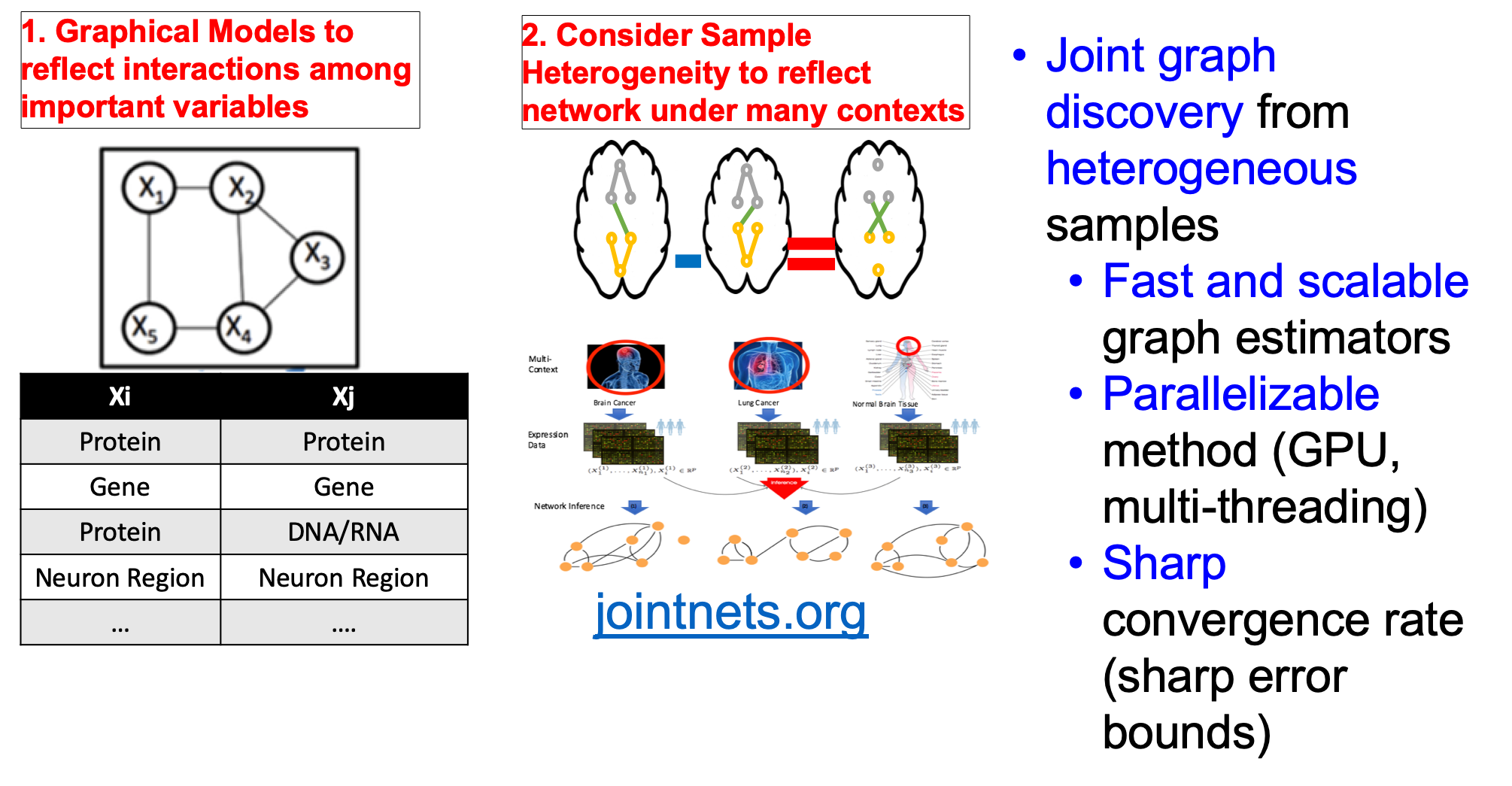
Technology revolutions in the past decade have collected large-scale heterogeneous samples from many scientific domains. For instance, genomic technologies have delivered petabytes of molecular measurements across more than hundreds of types of cells and tissues from national projects like ENCODE and TCGA. Neuroimaging technologies have generated petabytes of functional magnetic resonance imaging (fMRI) datasets across thousands of human subjects (shared publicly through projects like openfMRI). Given such data, understanding and quantifying variable graphs from heterogeneous samples (about multiple contexts) is a fundamental analysis task.
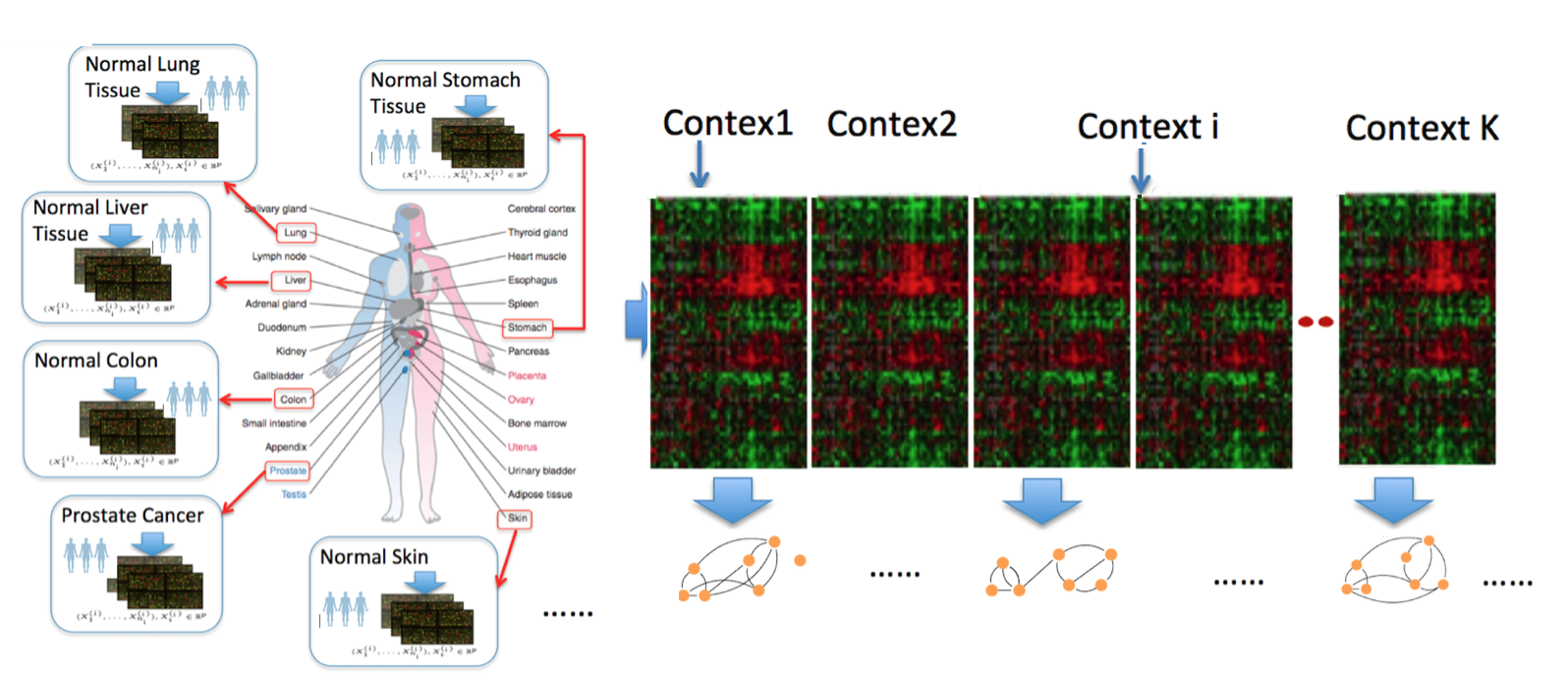
Such variable graphs can significantly simplify network-driven studies about diseases, can help understand the neural characteristics underlying clinical disorders and can allow for understanding genetic or neural pathways and systems. The number of contexts (denoted as $K$) that those applications need to consider grows extremely fast, ranging from tens (e.g., cancer types in TCGA) to thousands (e.g., number of subjects in openfMRI~). The number of variables (denoted as $p$) ranges from hundreds (e.g., number of brain regions) to tens of thousands (e.g., number of human genes).
One typical approach to tackle the above data analysis problem is to jointly estimate $K$ different but related conditional dependency graphs through a multi-task formulation of the sparse Gaussian Graphical Model (multi-sGGM). Most current studies of multi-sGGMs, however, involve expensive and difficult non-smooth optimizations, making them difficult to scale up to many dimensions (large $p$) or with many contexts (large $K$).
Four different types of tasks
We aim to fill this gap and have designed a category of novel estimators that can achieve fast and scalable joint structure estimation of multiple sGGMs. There exist four important tasks when learning multi-sGGMs from heterogeneous samples:
- (1) Learning task-specific edges explicitly. Explicitly quantifying the context-specific substructures involves a very challenging optimization task under the traditional MLE based multi-sGGMs formulation.
- (2) Estimating the change of variable dependencies directly. The second category aims to estimate changes in the dependency structure of two $p$-dimensional Gaussian Graphical Model (GGMs), based on $n_c$ and $n_d$ samples from two contexts respectively. For instance, on samples from a controlled disease study, ‘c’ may represent the ‘‘control’ group and ‘d’ for ‘‘disease’.
- (3) Incorporating existing knowledge of the variable nodes or knowledge of the relationships among nodes. In addition to the samples themselves, additional information is widely available in real-world applications, including for instance the spatial and anatomical evidence of brain regions when estimating the functional brain connectivity networks from fMRI samples).
- (4) Enforcing graph relatedness through structural norms. The first type of multi-sGGMs seeks to optimize a sparsity regularized data likelihood function plus an extra norm function to enforce structural similarity among the multiple networks to be estimated.
Targeting each challenge, our work introduces estimators that are both computationally efficient and theoretically guaranteed. The website JointNets.org introduces the suite of tools we have developed for helping researchers effectively translate aggregated data into knowledge that take the form of graphs.
Background: Sparse Gaussian Graphical Model (sGGM) and multi-sGGMs
The sparse Gaussian Graphical Model(sGGM) assumes data samples are independently and identically drawn from a multivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$. The graph structure $G$ among $p$ features is encoded by the sparsity pattern of the inverse covariance matrix, also named precision matrix, $\Omega$.
In $G$ an edge does not connect $j$-th node and $k$-th node (i.e., conditional independent) if and only if $\Omega_{jk} = 0$. sGGM imposes a sparse L1 penalty on the $\Omega$.
Modern multi-context molecular datasets are high dimensional, heterogeneous and noisy. For such heterogeneous data samples, rather than estimating sGGM of each condition separately, a multi-task formulation that jointly estimates $K$ different but related sGGMs can lead to a better generalization.
A list of Our Tools for Joint learning of Multiple Sparse Gaussian Graphical Model (multi-sGGM) in a Scalable Way
We have designed a suite of novel and fast machine-learning algorithms to identify context-specific interaction graphs from such data.
So far, we have released multiple methods in the following table. We have their corresponding prototype tools into one joint R toolkit jointNets in CRAN.
-
More details on JointNets Tools toolkit.
| No. | Tool Name | Short Description | Venue |
|---|---|---|---|
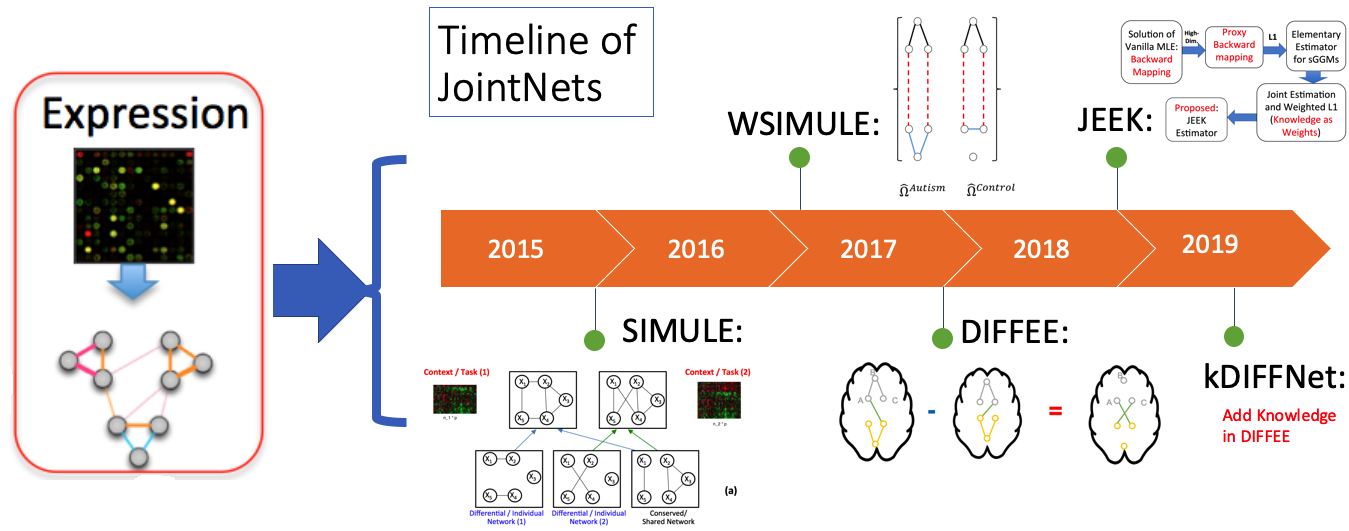
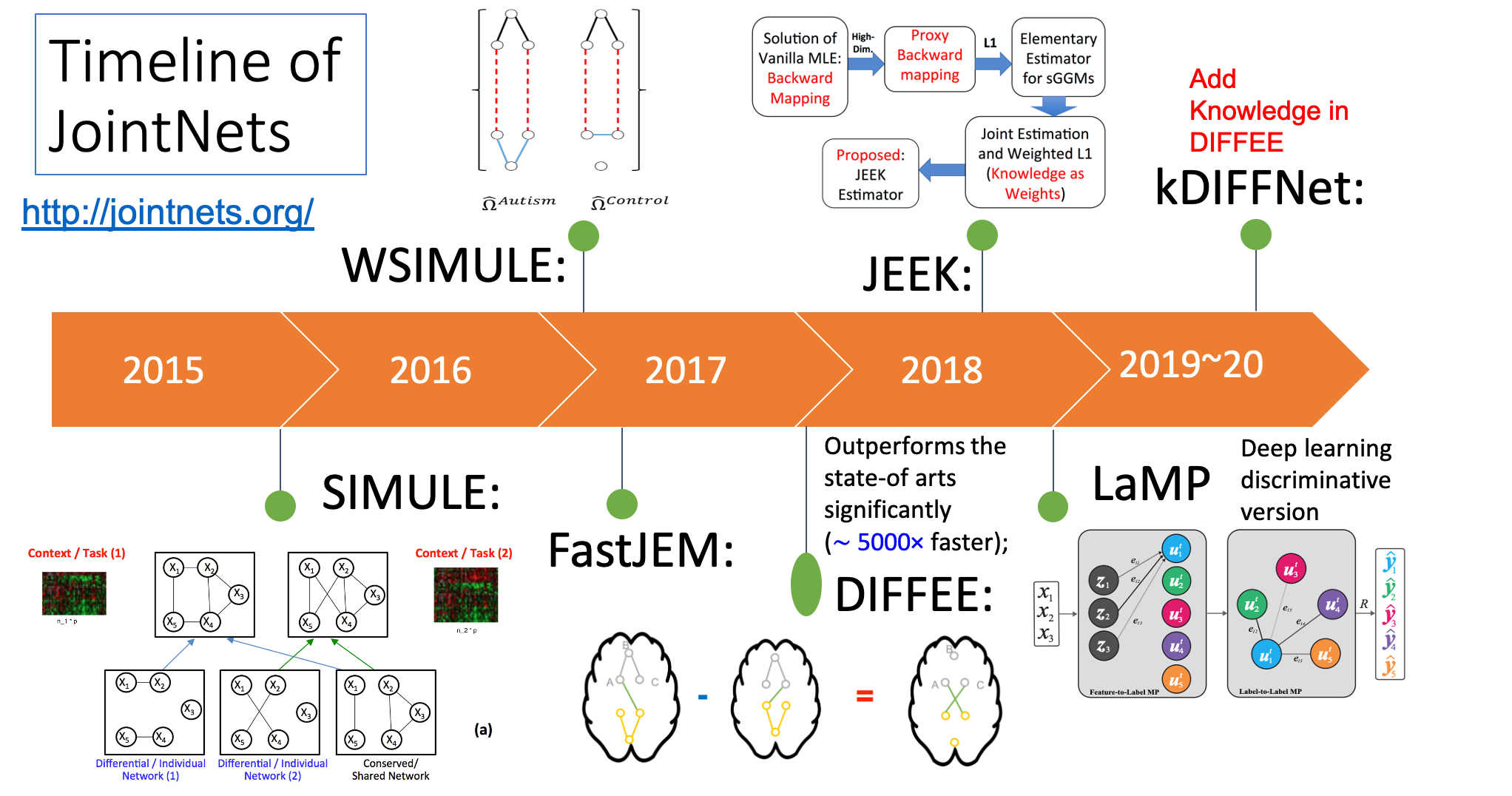
| 1 | SIMULE | A constrained L1 minimization approachfor estimating multiple Sparse **Gaussian or Nonparanormal** Graphical Models | MachineLearning 17 |
| 2 | W-SIMULE | A Constrained, Weighted-L1 Minimization Approach for Joint Discovery of **Heterogeneous Neural Connectivity** Graphs with Additional Prior knowledge | NIPS17 Network workshop |
| 3 | JEEK | Fast and Scalable Joint Estimator for **Integrating Additional Knowledge** in Learning Multiple Related Sparse Gaussian Graphical Models | ICML18 |
| 4 | FASJEM | A Fast and Scalable Joint Estimator for Learning **Multiple Related** Sparse Gaussian Graphical Models | AISTAT17 |
| 5 | DIFFEE | Fast~and~Scalable Learning of **Sparse Changes** in High-Dimensional Gaussian Graphical Model Structure | AISTAT18 |
| 6 | LaMP | Graph Neural Networks for Generating **Discriminative Relational Graphs** among Labels fpr Classification | ECML2018 |
| 7 | kDIFFNet | Adding Knowledge in DIFFEE Fast~and~Scalable Learning of **Sparse Changes** in High-Dimensional Gaussian Graphical Model Structure | UnderReview |
| 8 | C-Trans | General Multi-label Image Classification with **Transformers** | UnderReview |
Contact
Have questions or suggestions? Feel free to ask me on Twitter or email me.
Thanks for reading!