MultiGraphs (Index of Posts):
12 May 2018
Paper: Most updated version at HERE | Previous version: @Arxiv |
TalkSlide: URL
R package: URL
GitRepo for R package: URL
install.packages("jeek")
library(jeek)
demo(jeek)
Abstract
We consider the problem of including additional knowledge in estimating sparse Gaussian graphical models (sGGMs) from aggregated samples, arising often in bioinformatics and neuroimaging applications. Previous joint sGGM estimators either fail to use existing knowledge or cannot scale-up to many tasks (large $K$) under a high-dimensional (large $p$) situation. In this paper, we propose a novel \underline{J}oint \underline{E}lementary \underline{E}stimator incorporating additional \underline{K}nowledge (JEEK) to infer multiple related sparse Gaussian Graphical models from large-scale heterogeneous data. Using domain knowledge as weights, we design a novel hybrid norm as the minimization objective to enforce the superposition of two weighted sparsity constraints, one on the shared interactions and the other on the task-specific structural patterns. This enables JEEK to elegantly consider various forms of existing knowledge based on the domain at hand and avoid the need to design knowledge-specific optimization. JEEK is solved through a fast and entry-wise parallelizable solution that largely improves the computational efficiency of the state-of-the-art $O(p^5K^4)$ to $O(p^2K^4)$. We conduct a rigorous statistical analysis showing that JEEK achieves the same convergence rate $O(\log(Kp)/n_{tot})$ as the state-of-the-art estimators that are much harder to compute.
Empirically, on multiple synthetic datasets and two real-world data, JEEK outperforms the speed of the state-of-arts significantly while achieving the same level of prediction accuracy.
About Adding Additional Knowledge
One significant caveat of state-of-the-art joint sGGM estimators is the fact that little attention has been paid to incorporating existing knowledge of the nodes or knowledge of the relationships among nodes in the models.
In addition to the samples themselves, additional information is widely available in real-world applications. In fact, incorporating the knowledge is of great scientific interest. A prime example is when estimating the functional brain connectivity networks among brain regions based on fMRI samples, the spatial position of the regions are readily available. Neuroscientists have gathered considerable knowledge regarding the spatial and anatomical evidence underlying brain connectivity (e.g., short edges and certain anatomical regions are more likely to be connected \cite{watts1998collective}). Another important example is the problem of identifying gene-gene interactions from patients’ gene expression profiles across multiple cancer types. Learning the statistical dependencies among genes from such heterogeneous datasets can help to understand how such dependencies vary from normal to abnormal and help to discover contributing markers that influence or cause the diseases. Besides the patient samples, state-of-the-art bio-databases like HPRD \cite{prasad2009human} have collected a significant amount of information about direct physical interactions among corresponding proteins, regulatory gene pairs or signaling relationships collected from high-qualify bio-experiments.
Although being strong evidence of structural patterns we aim to discover, this type of information has rarely been considered in the joint sGGM formulation of such samples. This paper aims to fill this gap by adding additional knowledge most effectively into scalable and fast joint sGGM estimations.
The proposed JEEK estimator provides the flexibility of using ($K+1$) different weight matrices representing the extra knowledge. We try to showcase a few possible designs of the weight matrices, including (but not limited to):
- Spatial or anatomy knowledge about brain regions;
- Knowledge of known co-hub nodes or perturbed nodes;
- Known group information about nodes, such as genes belonging to the same biological pathway or cellular location;
- Using existing known edges as the knowledge, like the known protein interaction databases for discovering gene networks (a semi-supervised setting for such estimations).
We sincerely believe the scalability and flexibility provided by JEEK can make structure learning of joint sGGM feasible in many real-world tasks.
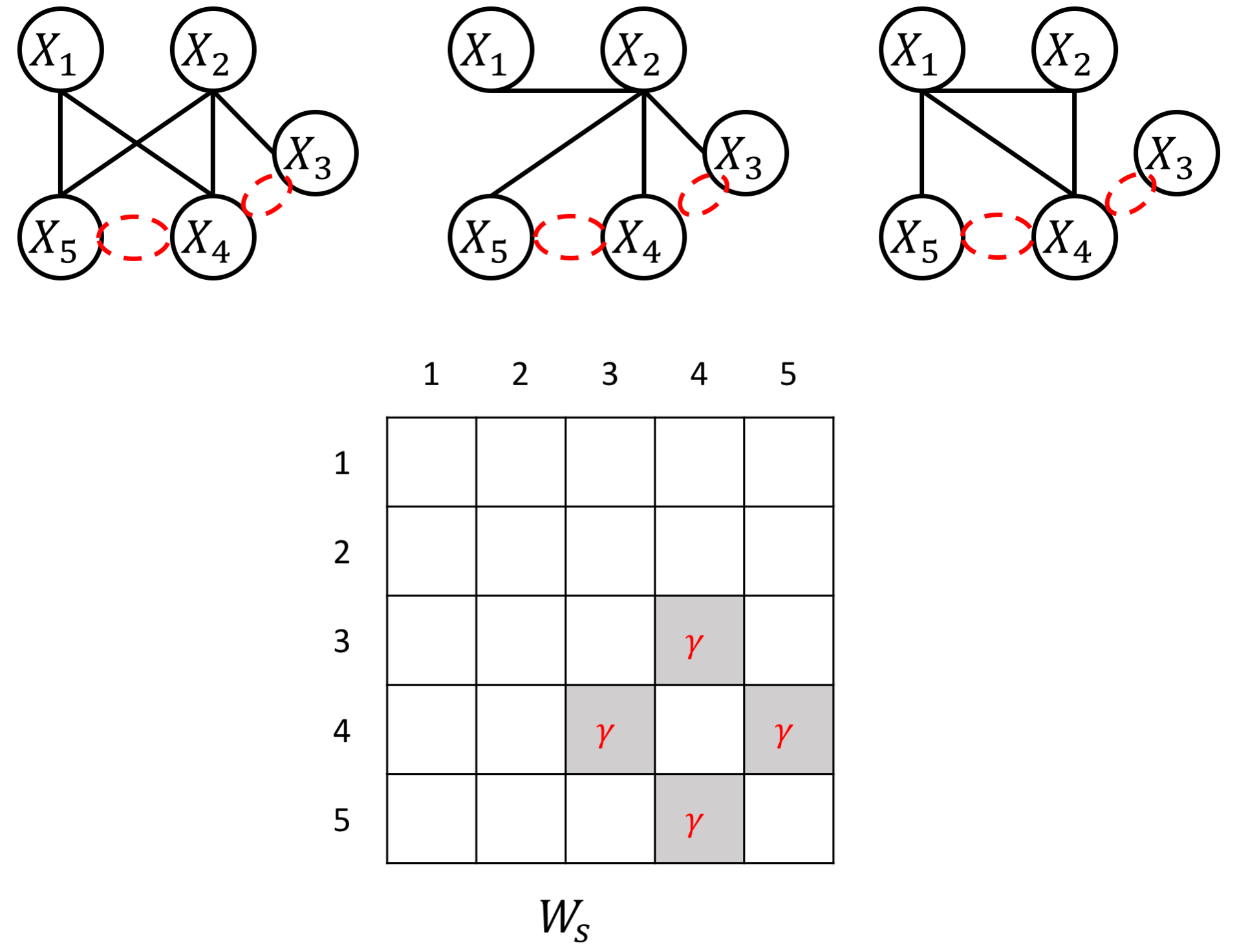
an example W for how to add known group sparity
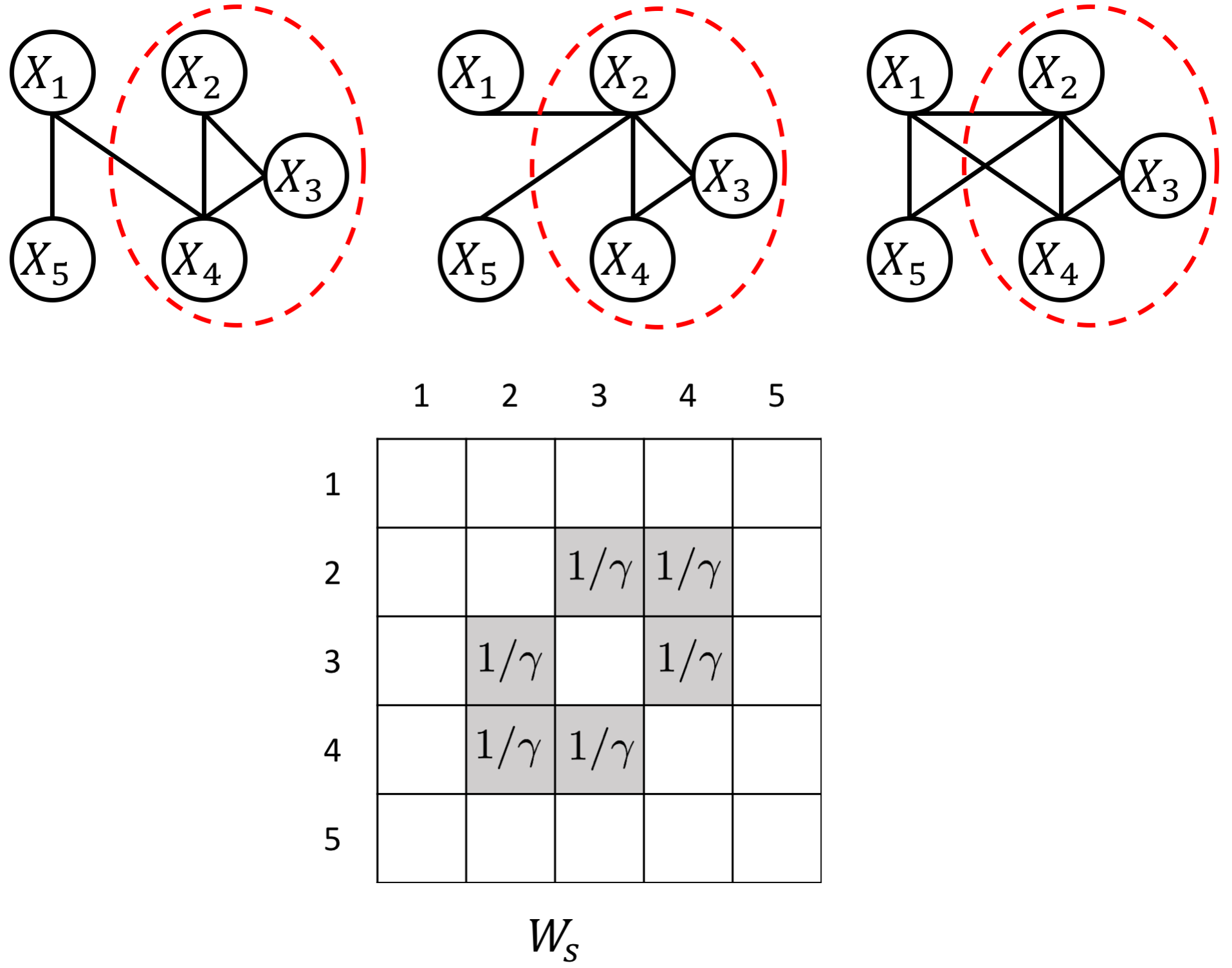
an example W for how to add known group interactions
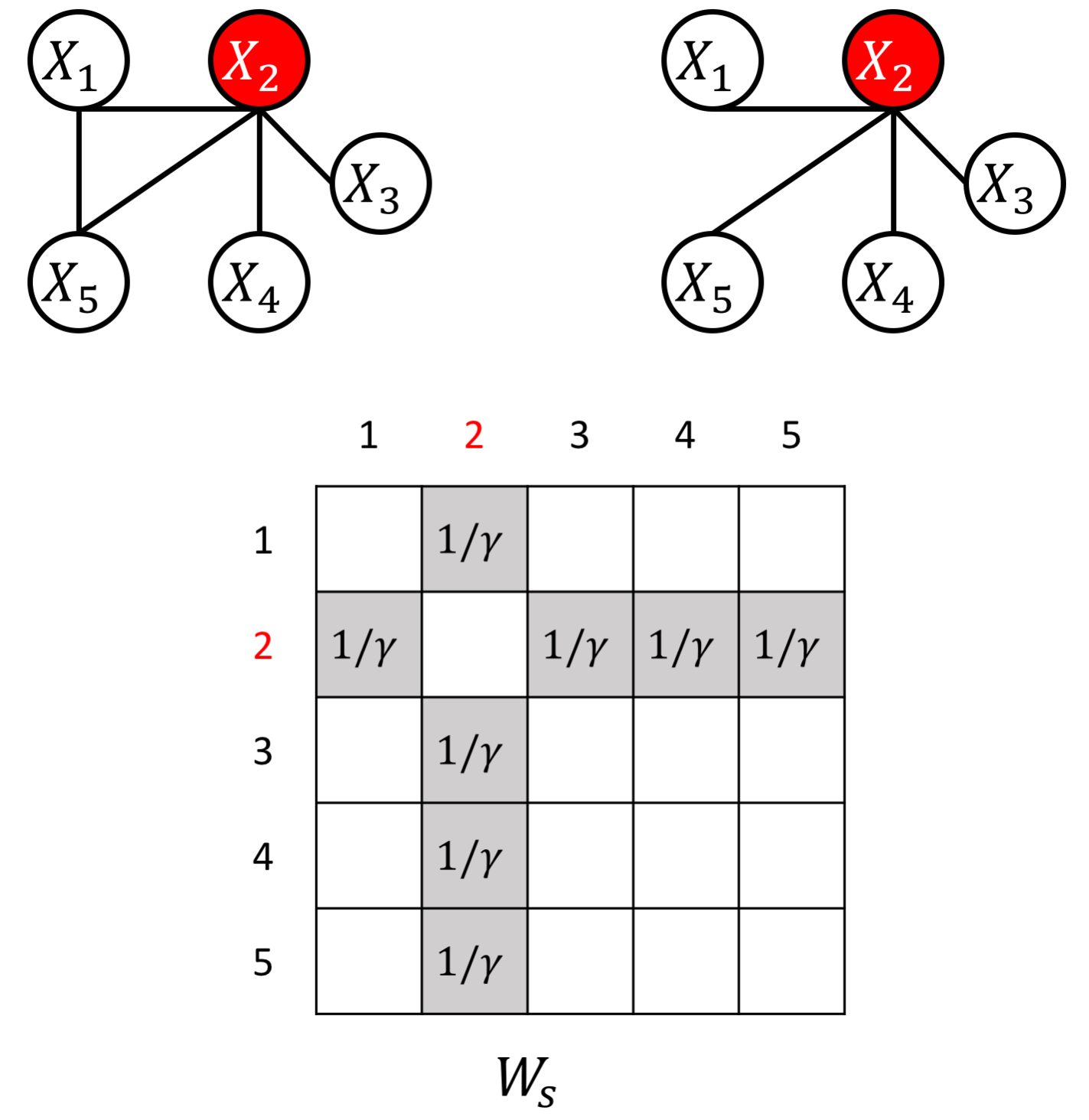
an example W for how to add known hub node
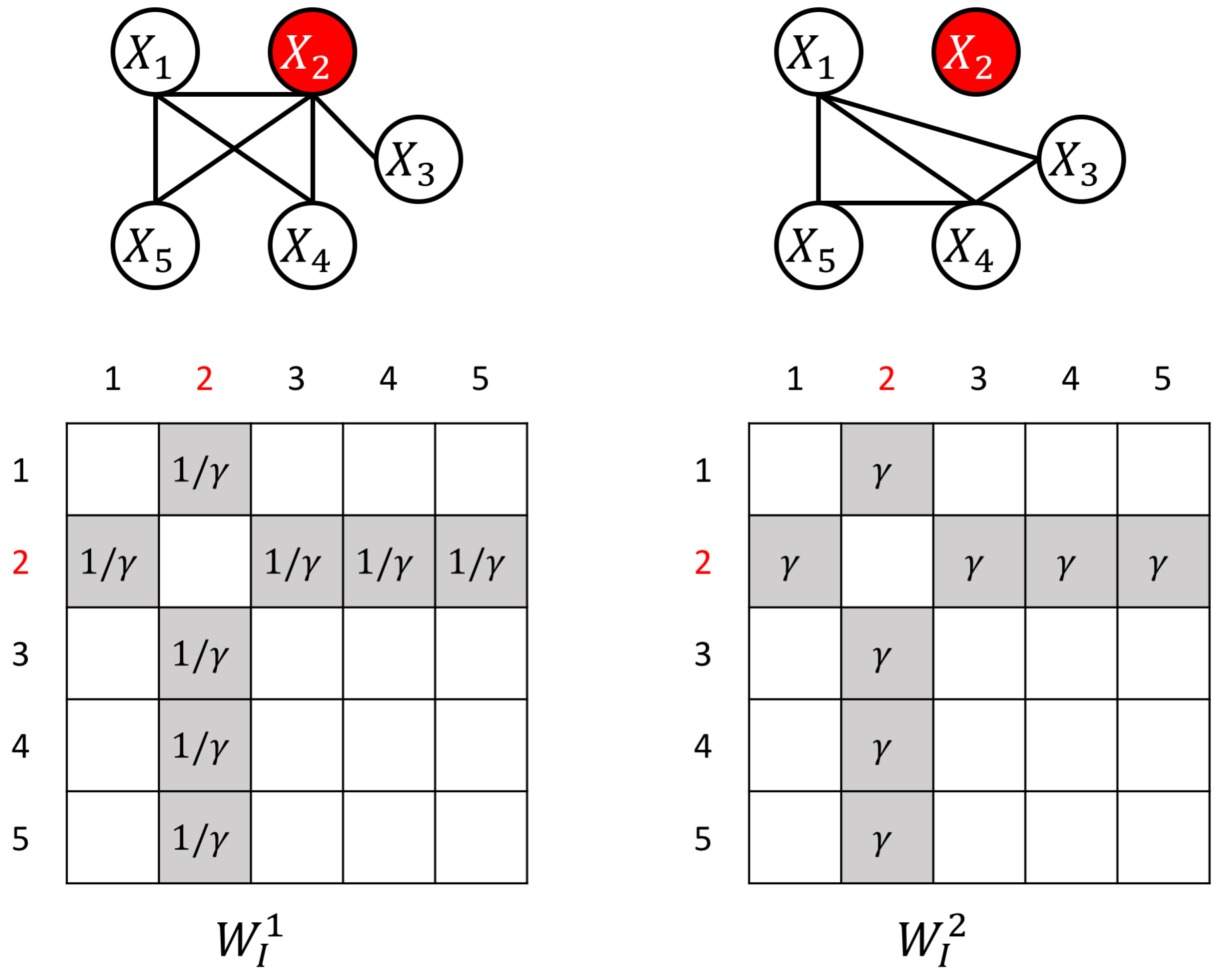
an example W for how to add known perturbed-hub node
Citations
@conference{wang2018jeek,
Author = {Wang, Beilun and Sekhon, Arshdeep and Qi, Yanjun},
Booktitle = {Proceedings of The 35th International Conference on Machine Learning (ICML)},
Title = {A Fast and Scalable Joint Estimator for Integrating Additional Knowledge in Learning Multiple Related Sparse Gaussian Graphical Models},
Year = {2018}}
}
Having trouble with our tools? Please contact Beilun and we’ll help you sort it out.
08 Sep 2017
We are updating the R package: simule with one more function: W-SIMULE
install.packages("simule")
library(simule)
demo(wsimule)
Paper: @Arxiv @ NIPS 2017 workshop for Advances in Modeling and Learning Interactions from Complex Data.
Abstract
Determining functional brain connectivity is crucial to understanding the brain and neural differences underlying disorders such as autism. Recent studies have used Gaussian graphical models to learn brain connectivity via statistical dependencies across brain regions from neuroimaging. However, previous studies often fail to properly incorporate priors tailored to neuroscience, such as preferring shorter connections. To remedy this problem, the paper here introduces a novel, weighted-ℓ1, multi-task graphical model (W-SIMULE). This model elegantly incorporates a flexible prior, along with a parallelizable formulation. Additionally, W-SIMULE extends the often-used Gaussian assumption, leading to considerable performance increases. Here, applications to fMRI data show that W-SIMULE succeeds in determining functional connectivity in terms of (1) log-likelihood, (2) finding edges that differentiate groups, and (3) classifying different groups based on their connectivity, achieving 58.6\% accuracy on the ABIDE dataset. Having established W-SIMULE’s effectiveness, it links four key areas to autism, all of which are consistent with the literature. Due to its elegant domain adaptivity, W-SIMULE can be readily applied to various data types to effectively estimate connectivity.

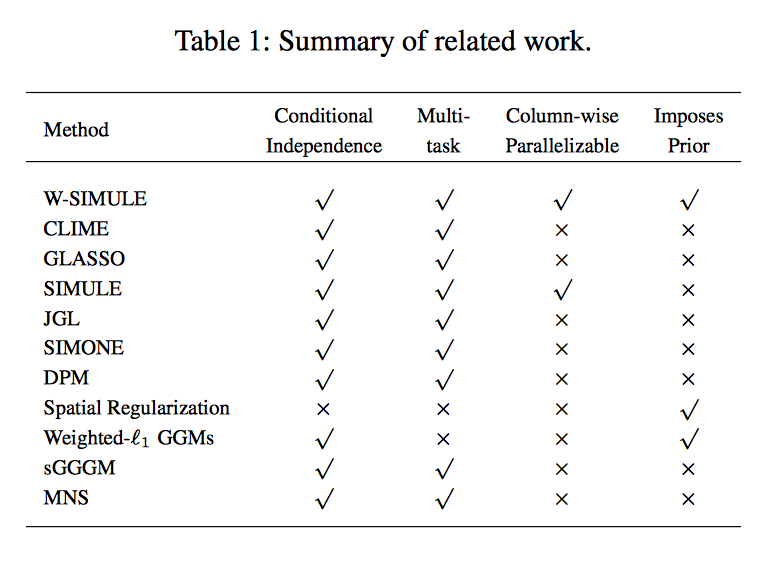
Citations
@article{singh2017constrained,
title={A Constrained, Weighted-L1 Minimization Approach for Joint Discovery of Heterogeneous Neural Connectivity Graphs},
author={Singh, Chandan and Wang, Beilun and Qi, Yanjun},
journal={arXiv preprint arXiv:1709.04090},
year={2017}
}
Having trouble with our tools? Please contact Beilun and we’ll help you sort it out.
01 Jun 2016
install.packages("fasjem")
library(fasjem)
demo(fasjem)
Abstract
Estimating multiple sparse Gaussian Graphical
Models (sGGMs) jointly for many related
tasks (large K) under a high-dimensional
(large p) situation is an important task.
Most previous studies for the joint estimation
of multiple sGGMs rely on penalized
log-likelihood estimators that involve expensive
and difficult non-smooth optimizations.
We propose a novel approach, FASJEM for
fast and scalable joint structure-estimation of
multiple sGGMs at a large scale. As the first
study of joint sGGM using the M-estimator
framework, our work has three major contributions:
(1) We solve FASJEM through an
entry-wise manner which is parallelizable. (2)
We choose a proximal algorithm to optimize
FASJEM. This improves the computational
efficiency from O(Kp3
) to O(Kp2
) and reduces
the memory requirement from O(Kp2
)
to O(K). (3) We theoretically prove that FASJEM
achieves a consistent estimation with
a convergence rate of O(log(Kp)/ntot). On
several synthetic and four real-world datasets,
FASJEM shows significant improvements over
baselines on accuracy, computational complexity
and memory costs.
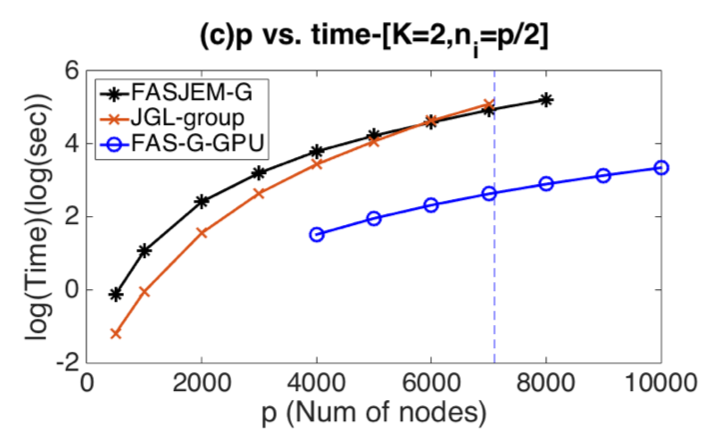

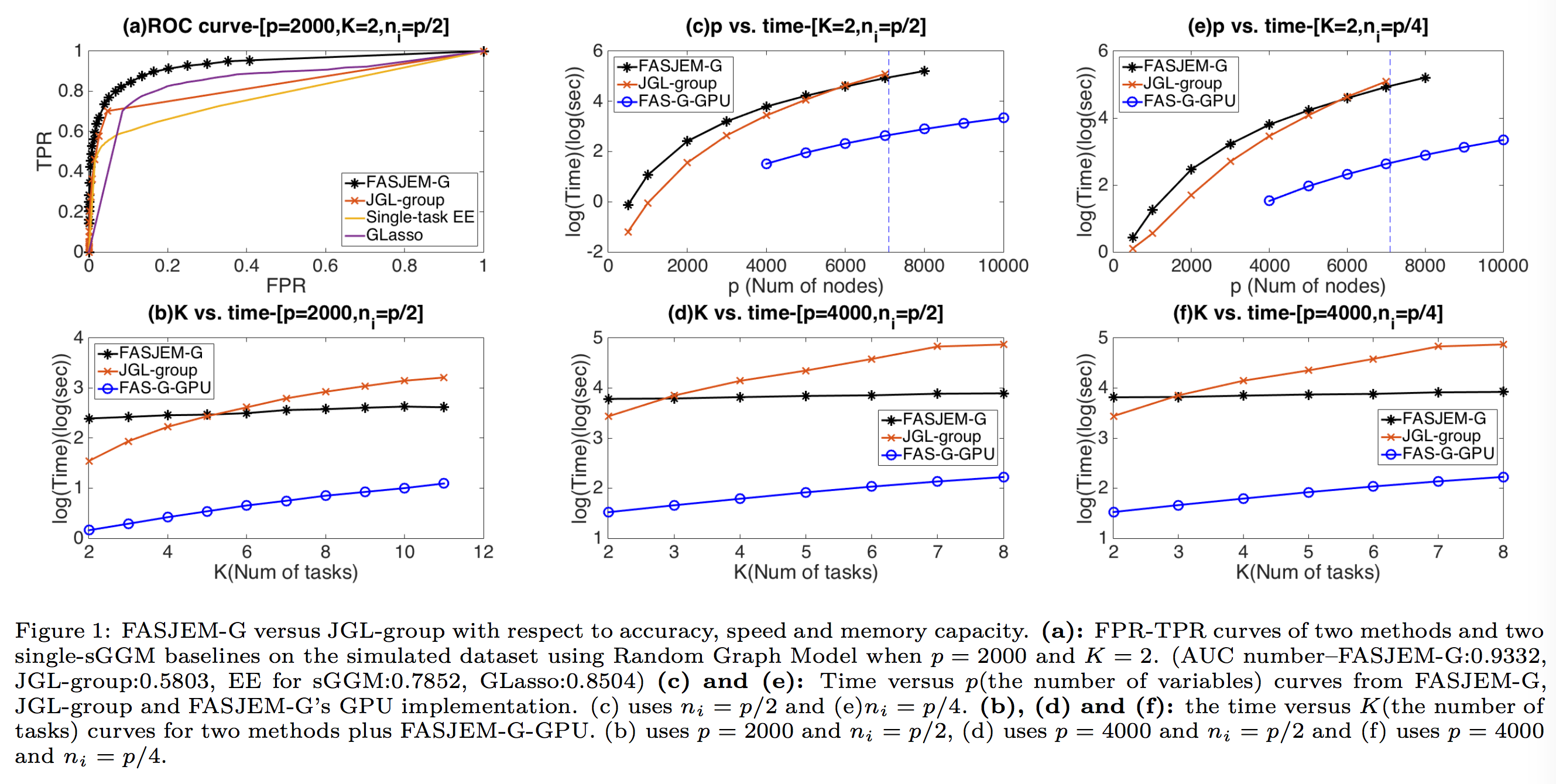
Citations
@inproceedings{wang2017fast,
title={A Fast and Scalable Joint Estimator for Learning Multiple Related Sparse Gaussian Graphical Models},
author={Wang, Beilun and Gao, Ji and Qi, Yanjun},
booktitle={Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, PMLR:, 2017.},
volume={54},
pages={1168--1177},
year={2017}
}
Having trouble with our tools? Please contact Beilun and we’ll help you sort it out.
08 May 2016
install.packages("simule")
library(simule)
demo(simule)
Abstract
Identifying context-specific entity networks from aggregated data is an important task, arising often in bioinformatics and neuroimaging. Computationally, this task can be formulated as jointly estimating multiple different, but related, sparse Undirected Graphical Models (UGM) from aggregated samples across several contexts. Previous joint-UGM studies have mostly focused on sparse Gaussian Graphical Models (sGGMs) and can’t identify context-specific edge patterns directly. We, therefore, propose a novel approach, SIMULE (detecting Shared and Individual parts of MULtiple graphs Explicitly) to learn multi-UGM via a constrained L1 minimization. SIMULE automatically infers both specific edge patterns that are unique to each context and shared interactions preserved among all the contexts. Through the L1 constrained formulation, this problem is cast as multiple independent subtasks of linear programming that can be solved efficiently in parallel. In addition to Gaussian data, SIMULE can also handle multivariate Nonparanormal data that greatly relaxes the normality assumption that many real-world applications do not follow. We provide a novel theoretical proof showing that SIMULE achieves a consistent result at the rate O(log(Kp)/n_{tot}). On multiple synthetic datasets and two biomedical datasets, SIMULE shows significant improvement over state-of-the-art multi-sGGM and single-UGM baselines.
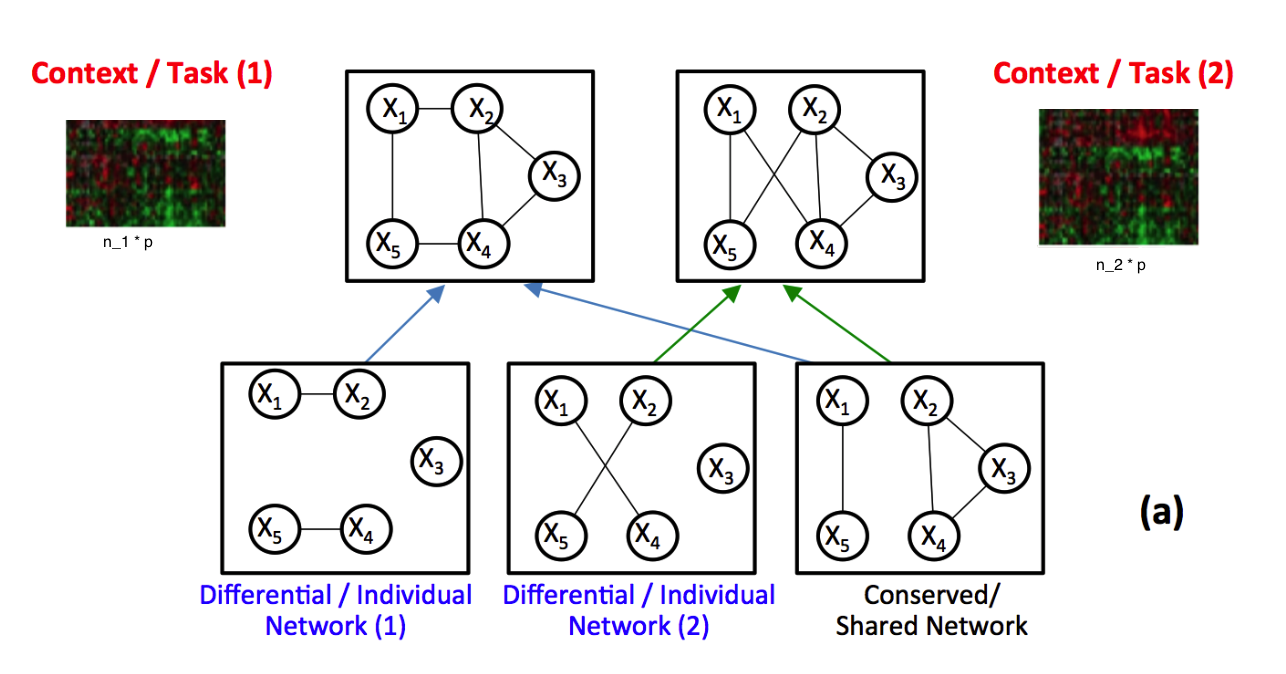
Citations
@Article{Wang2017,
author="Wang, Beilun and Singh, Ritambhara and Qi, Yanjun",
title="A constrained L1 minimization approach for estimating multiple sparse Gaussian or nonparanormal graphical models",
journal="Machine Learning",
year="2017",
month="Oct",
day="01",
volume="106",
number="9",
pages="1381--1417",
abstract="Identifying context-specific entity networks from aggregated data is an important task, arising often in bioinformatics and neuroimaging applications. Computationally, this task can be formulated as jointly estimating multiple different, but related, sparse undirected graphical models(UGM) from aggregated samples across several contexts. Previous joint-UGM studies have mostly focused on sparse Gaussian graphical models (sGGMs) and can't identify context-specific edge patterns directly. We, therefore, propose a novel approach, SIMULE (detecting Shared and Individual parts of MULtiple graphs Explicitly) to learn multi-UGM via a constrained L1 minimization. SIMULE automatically infers both specific edge patterns that are unique to each context and shared interactions preserved among all the contexts. Through the L1 constrained formulation, this problem is cast as multiple independent subtasks of linear programming that can be solved efficiently in parallel. In addition to Gaussian data, SIMULE can also handle multivariate Nonparanormal data that greatly relaxes the normality assumption that many real-world applications do not follow. We provide a novel theoretical proof showing that SIMULE achieves a consistent result at the rate
log (Kp)/(n_tot). On multiple synthetic datasets and two biomedical datasets, SIMULE shows significant improvement over state-of-the-art multi-sGGM and single-UGM baselines
(SIMULE implementation and the used datasets @ https://github.com/QData/SIMULE ).",
issn="1573-0565",
doi="10.1007/s10994-017-5635-7",
url="https://doi.org/10.1007/s10994-017-5635-7"
}
Having trouble with our tools? Please contact Beilun and we’ll help you sort it out.









